Phần trước: [Lý thuyết đồ thị cơ bản] Phần 3: Tìm kiếm theo chiều sâu trên đồ thị - Depth-First Search (DFS)

Đường đi ngắn nhất trên đồ thị

Nếu đồ thị biểu diễn một mạng lưới giao thông, thì người ta không chỉ quan tâm tới việc có tồn tại đường đi từ một đỉnh này tới đỉnh khác hay không, mà người ta còn quan tâm tới con đường tối ưu nhất, ngắn nhất có thể.

Trong lý thuyết đồ thị, bài toán đường đi ngắn nhất giữa hai đỉnh cho trước là bài toán tìm một đường đi giữa chúng sao cho tổng các trọng số của các cạnh tạo nên đường đi đó là nhỏ nhất. Định nghĩa một cách hình thức, cho trước một đồ thị có trọng số \( G = (V, E, w) \) (nghĩa là một tập đỉnh V, một tập cạnh E, và một hàm trọng số có giá trị thực w : E → R), cho trước một đỉnh u thuộc V, tìm một đường đi P từ u tới một đỉnh v thuộc V sao cho:

nhỏ nhất trong tất cả các đường đi từ u tới v. Bài toán đường đi ngắn nhất giữa mọi cặp đỉnh là một bài toán tương tự, trong đó ta phải tìm các đường đi ngắn nhất cho mọi cặp đỉnh u và v.

Các thuật toán thường được dùng để giải quyết những bài toán này là:

• Thuật toán Dijkstra - giải bài toán bài toán đường đi ngắn nhất giữa hai đỉnh cho trước nếu tất cả các trọng số đều không âm. Thuật toán này có thể tính toán tất cả các đường đi ngắn nhất từ một đỉnh xuất phát cho trước s tới mọi đỉnh khác mà không làm tăng thời gian chạy.
• Thuật toán Bellman-Ford - giải bài toán bài toán đường đi ngắn nhất giữa hai đỉnh cho trước trong trường hợp trọng số có thể có giá trị âm.
• Giải thuật tìm kiếm A* giải bài toán bài toán đường đi ngắn nhất giữa hai đỉnh cho trước sử dụng heuristics để tăng tốc độ tìm kiếm
• Thuật toán Floyd-Warshall - giải bài toán đường đi ngắn nhất cho mọi cặp đỉnh.
• Thuật toán Johnson - giải bài toán đường đi ngắn nhất cho mọi cặp đỉnh, có thể nhanh hơn thuật toán Floyd-Warshall trên các đồ thị thưa.
• Lý thuyết nhiễu (Perturbation theory) - tìm đường đi ngắn nhất địa phương (trong trường hợp xấu nhất)

Chú ý:

Ta có đường đi P = {v1, v2, …, vk} là một đường đi ngắn nhất từ v1 tới vk. Khi đó ta có nhận xét, đường đi từ vi tới vj qua {vi, vi+1, …, vj} với i,j ∈ [1, k] là một đường đi ngắn nhất từ vi tới vj.

Thuật toán Dijkstra

Trong trường hợp đồ thị \( G = (V, E, w) \) có trọng số trên các cạnh không âm, ta có thuật toán Dijkstra để tìm đường đi ngắn nhất từ đỉnh xuất phát s tới các đỉnh khác của đồ thị.

Ý tưởng của thuật toán:

Ta có mảng kc[u] là khoảng cách ngắn nhất từ đỉnh s tới đỉnh u trên đồ thị. Ban đầu kc[s] = 0, các giá trị khác bằng dương vô cực. Ta sẽ lấy đỉnh u có kc[u] nhỏ nhất vào thời điểm hiện tại, và sử dụng khoảng cách của nó để cập nhật khoảng cách ngắn nhất của các đỉnh xung quanh. Với một đỉnh u bất kì, vì nó được cập nhật bởi các đường đi ngắn nhất của các đỉnh xung quanh nó, nên bản thân đường đi của nó cũng là ngắn nhất.

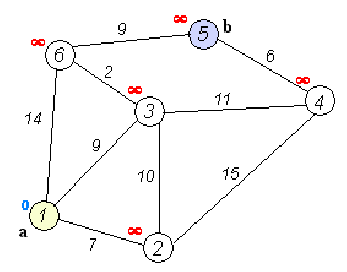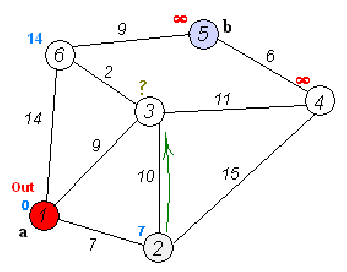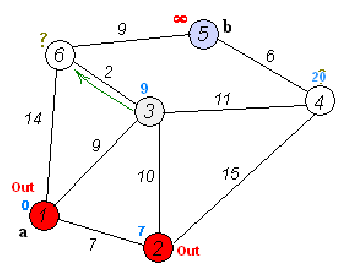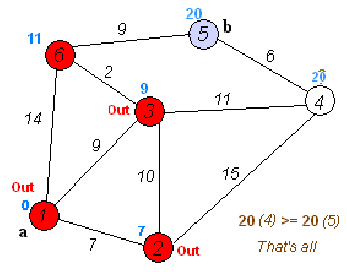
Dữ liệu:

• Đồ thị được biểu diễn bằng danh sách kề với một mảng vector g[maxn] với g[u] lưu các đỉnh kề của u kèm theo trọng số
• Mảng kc dùng để lưu trữ độ dài đường đi ngắn nhất từ đỉnh nguồn s đến đỉnh u.
• Để tính được giá trị nhỏ nhất này, khi khởi tạo ta phải gán cho kc[u] = +∞ (khi cài đặt trên máy tính, ta chỉ cần đặt bằng một giá trị cực lớn), sau đó gặp giá trị nhỏ hơn thì thay thế lại.
• Những đỉnh đã tính được kc[u] hữu hạn được cho vào một hàng đợi có ưu tiên. Hàng đợi này luôn được bổ sung và sắp xếp lại bằng một cấu trúc hợp lý (heap, set,…)
• Để theo dõi trạng thái của các đỉnh trong quá trình xét, ta dùng hàm cl. Lúc đầu các đỉnh được tô màu trắng (cl[u]=0), khi đã tính xong khoảng cách nó được tô màu đen(cl[u] != 0).
• Nếu cần ghi lại đường đi ta sẽ phải dùng một hàm pre để chỉ đỉnh đứng ngay trước đỉnh u trên đường đi ngắn nhất từ s tới u.

Cài đặt bằng ngôn ngữ C++ dùng set:

#define fs first
#define sc second

typedef pair<int,int> II;
vector<II> g[maxn];
set<II> S;
int cl[maxn], kc[maxn];

void Dijkstra(int s) 
{
	memset(kc,0,sizeof(kc));
	cl[s]=1;
	S.insert(II(kc[s],s));
	while(!s.empty())
	{
		II t=*S.begin();
		S.erase(t);
		int u=t.sc;
		for(int i=0; i<S.size(); ++i)
		{
			int v=g[u][i].fs, L=g[u][i].sc;
			if(cl[v]==0)
			{
				cl[v]=1;
				kc[v]=kc[u]+L;
				S.insert(II(kc[v],v));
			} else if(kc[v]>kc[u]+L)
			{
				S.erase(II(kc[v],v));
				kc[v]=kc[u]+L;
				S.insert(II(kc[v],v));
			}
		}
	}
}

Độ phức tạp

Thuật toán Dijkstra bình thường sẽ có độ phức tạp là \( O(n^2+m) \), do ta phải duyệt n lần (đối với n đỉnh), mỗi lần duyệt lại phải duyệt qua n đỉnh để tìm đỉnh có kc[u] nhỏ nhất. Tuy nhiên ta có thể sử dụng kết hợp với cấu trúc heap hoặc set, khi đó độ phức tạp sẽ là \( O((m+n)log(n)) \), nếu dùng Fibonacci thì độ phức tạp giảm xuống còn \( O(m+nlog n) \). Trong đó m là số cạnh, n là số đỉnh của đồ thị đang xét (giới thiệu ở bài sau).

Bài tập ví dụ:

• QBSCHOOL. Lời giải tại đây.
• QBBUILD. Lời giải tại đây.
• NETACCEL. Lời giải tại đây.
• VDANGER.
• BESTSPOT.

Phần sau: [Lý thuyết đồ thị cơ bản] Phần 5: DAG và sắp xếp topo trên đồ thị